

Graphing Stretches and Compressions of y=\text\left(x+2\right)+1. Graph reflections of logarithmic functions.Which transformation produces a function that increases faster One of the key points that is commonly defined for transformations of a logarithmic function comes from finding the input that gives an output of y 1 y 1. Graph stretches and compressions of logarithmic functions. Both the vertical stretch and compression produce graphs that are increasing. Recommended order of transformation: (1) Horizontal Translation, (2) Horizontal Stretch (3) Horizontal Reflection (4) Vertical Reflection (5) Vertical.Multiplying a function by a constant greater than 1 has the. Dilations: Stretching and Compressing Graphs. Transformations are used to change the graph of a parent function into the graph of a more complex function. fx is a horizontal reflection (in the y-axis). Stretching a graph means to make the graph narrower or wider. 1 (c) Absolute Value Function (d) Square Root Function f(x) x2 3 33 1 f(x) x3 2 332 (e) Quadratic Function Figure 1. Since the horizontal stretch is affecting the phase shift pi/3 the actual phase shift is pi/6 as the horizontal sretch is 1/2. So the horizontal stretch is by factor of 1/2. They are caused by differing signs between parent and child functions.Ī stretch or compression is a function transformation that makes a graph narrower or wider. To stretch a function horizontally by factor of n the transformation is just f (x/n). Reflections are transformations that result in a "mirror image" of a parent function. Solution for The graph shown to the right involves a reflection in the x-axis and/or a vertical stretch or shrink of a basic function. Reflecting a graph means to transform the graph in order to produce a "mirror image" of the original graph by flipping it across a line. All other functions of this type are usually compared to the parent function. Sketch the graph of each of the following transformations of y = xĪ stretch or compression is a function transformation that makes a graph narrower or wider, without translating it horizontally or vertically.įunction families are groups of functions with similarities that make them easier to graph when you are familiar with the parent function, the most basic example of the form.Ī parent function is the simplest form of a particular type of function. Graph each of the following transformations of y=f(x).
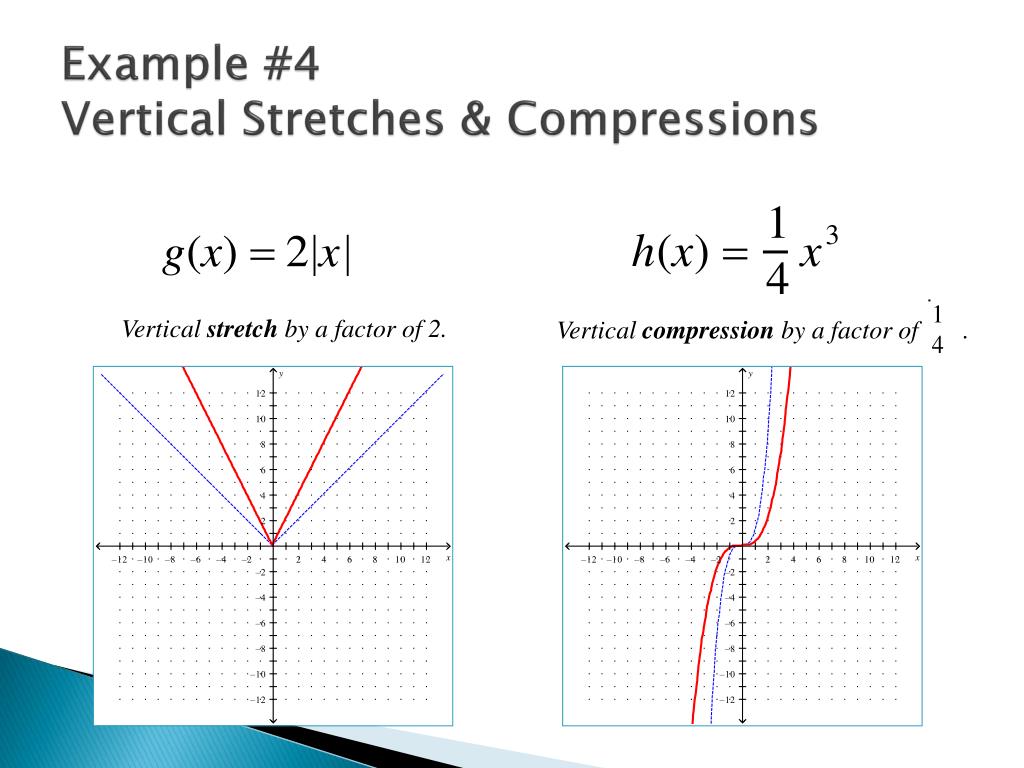

Vertical compressions and stretches of graph Vertical stretches of graphs. So, for any function when the output is multiplied by 1 it reflects across the xaxis. In general, g(x)1f(x), the graph of g is a reflection across the xaxis of the graph of f.
A negative a reflects it, and if 0Vertical stretching reflection graph how to#
How to transform the graph of a function This depends on the direction you want to transoform. The graph of g(x)x 2 is a reflection of f(x)x 2 across the xaxis. The parabola is translated (c,d) units, b reflects across y, but this just reflects it across the axis of symmetry, so it would look the same. Let y=f(x) be the function defined by the line segment connecting the points (-1, 4) and (2, 5). A quadratic equation is an equation of the form y ax2 + bx + c, where a, b and c are constants. Enter a function and you may move, stretch or shrink it.


 0 kommentar(er)
0 kommentar(er)
